Restriction (mathematics)

In mathematics, the notion of restriction of a function is defined as follows:

If f : E → F is a function from E to F, and A is a subset of E, then the restriction of f to A is the (partial) function

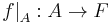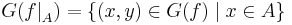{f|}_A�: A \to F having the graph G({f|}_A) = \{ (x,y)\in G(f) \mid x\in A \}.

(In rough words, it is "the same function", but only defined on 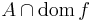A\cap \mathrm{dom} \, f.)

More generally, the restriction (or domain restriction or left-restriction) A ◁ R of a binary relation R between E and F may be defined as a relation having domain A, codomain F and graph G(A ◁ R) = {(x, y) ∈ G(R) | x ∈ A}. Similarly, one can define a right-restriction or range restriction R ▷ B. (Indeed, one could define a restriction to a subset of E x F, and the same applies to n-ary relations. These cases do not fit into the scheme of sheaves.)

The domain anti-restriction of a function or binary relation R (with domain E and codomain F) by a set A may be defined as (E \ A) ◁ R; it removes all elements of A from the domain E. It is sometimes denoted A ⩤ R. The range anti-restriction R ⩥ B is defined by R ▷ (F \ B).

Examples

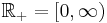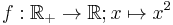  1. The restriction of the non-injective function f: \mathbb R\to\mathbb R; x\mapsto x^2 to \mathbb R_%2B=[0,\infty) is the injection f: \mathbb R_%2B\to\mathbb R; x\mapsto x^2.
  2. The inclusion map of a set A into a superset E of A is the restriction of the identity function on E to A.

See also